Still Image
Compression
Let us first see the difference between data compression and bandwidth compression.
Data compression refers to the process of
reducing the digital source data to a desired
level. On the other hand, bandwidth
compression refers to the process of reducing the
analog bandwidth of the analog source. What
do we really mean by these terms? Here
is an example. Consider the conventional wire
line telephony. A subscriber’s voice
is filtered by a lowpass filter to limit the
bandwidth to a nominal value of 4 kHz. So,
the channel bandwidth is 4 kHz. Suppose that
it is converted to digital data for longdistance
transmission. As we will see later, in order
to reconstruct the original analog
signal that is band limited to 4 kHz exactly,
sampling theory dictates that one should
have at least 8000 samples per second.
Additionally, for digital transmission each
analog sample must be converted to a digital
value. In telephony, each analog voice
sample is converted to an 8-bit digital
number using pulse code modulation
(PCM).
Therefore, the voice data rate that a
subscriber originates is 64,000 bits per second.
As we mentioned above, in an ideal case this
digital source will require 32 kHz of
bandwidth for transmission. Even if we employ
some form of data compression to
reduce the source rate to say, 16 kilobits
per second, it will still require at least 8 kHz
of channel bandwidth for real-time
transmission. Hence, data compression does not
necessarily reduce the analog bandwidth. Note
that the original analog voice requires
only 4 kHz of bandwidth. If we want to
compress bandwidth, we can simply filter
theanalog signal by a suitable filter with a
specified cutoff frequency to limit the
bandwidth occupied by the analog signal.
Figure 1Original
cameraman picture.
Having clarified the terms data compression and bandwidth
compression, let us
look into some basic data compression techniques known to us.
Henceforth, we will
use the terms compression and data compression interchangeably.
All image and
video sources have redundancies. In a still image, each pixel in a
row may have a
value very nearly equal to a neighboring pixel value. As an
example, consider the
cameraman picture shown in Figure 1. Figure 2
shows the profile (top figure)
Figure 2 Profile of
cameraman image along row number 164. The top graph shows pixel
intensity,
and the bottom graph shows corresponding normalized correlation over 128 pixel
displacements.
and the corresponding correlation (bottom figure) of the cameraman
picture along
row 164. The MATLAB M-file for generating Figure 1.4 is listed
below. Observe
that the pixel values are very nearly the same over a large number
of neighboring
pixels and so is the pixel correlation. In other words, pixels in
a row have a high correlation.
Similarly, pixels may also have a high correlation along the
columns. Thus,
pixel redundancies translate to pixel correlation. The basic
principle behind image
data compression is to decorrelatethe pixels
and encode the resulting decorrelated
image for transmission or storage. A specific compression scheme
will depend on
the method by which the pixel correlations are removed.
Figure1
4.m
%
Plots the image intensity profile and pixel correlation
%
along a specified row.
clear
close
all
I =
imread(’cameraman.tif’);
figure,imshow(I),title(’Input
image’)
%
Row =
164; % row number of image profile
x =
double(I(Row,:));
Col =
size(I,2);
%
MaxN =
128; % number of correlation points to calculate
Cor =
zeros(1,MaxN); % array to store correlation values
for k
= 1:MaxN
l =
length(k:Col);
Cor(k)
= sum(x(k:Col) .* x(1:Col-k+1))/l;
end
MaxCor
= max(Cor);
Cor =
Cor/MaxCor;
figure,subplot(2,1,1),plot(1:Col,x,’k’,’LineWidth’,2)
xlabel(’Pixel
number’), ylabel(’Amplitude’)
legend([’Row’
’ ’ num2str(Row)],0)
subplot(2,1,2),plot(0:MaxN-1,Cor,’k’,’LineWidth’,2)
xlabel(’Pixel
displacement’), ylabel(’Normalized corr.’)
One of the earliest and basic image compression techniques is
known as the differential
pulse code modulation (DPCM) [1]. If the pixel correlation along only one
dimension (row or column) is removed, then the DPCM is called
one-dimensional
(1D) DPCM or row-by-row DPCM. If the correlations along both
dimensions are
removed, then the resulting DPCM is known as 2D DPCM. A DPCM
removes
pixel correlation and requantizes the residual pixel values for
storage or transmission.
The
residual image has a variance much smaller than that of the original image.
Further, the residual image has a probability density function,
which is a doublesided
exponential function. These give rise to compression.
The quantizer is fixed no matter how the decorrelated pixel values
are. A variation
on the theme is to use quantizers that adapt to changing input
statistics, and therefore,
the corresponding DPCM is called an adaptive DPCM. DPCM is very
simple to
implement, but the compression achievable is about 4:1. Due to
limited bit width of
thequantizer for the residual image, edges are not preserved well
in the DPCM. It
also exhibits occasional streaks across the image when channel
error occurs.We will
discuss DPCM in detail in a later chapter.
Another popular and more efficient compression scheme is known by
the generic
nametransform coding. Remember that the idea is to reduce or
remove pixel correlation
to achieve compression. In transform coding, a block of image
pixels is linearly
transformed into another block of transform coefficients of the same size as the pixel
block with the hope that only a few of the transform coefficients
will be significant
and the rest may be discarded. This implies that storage space is
required to store
only the significant transform coefficients, which are a fraction
of the total number
of coefficients and hence the compression. The original image can
be reconstructed
by performing the inverse transform of the reduced coefficient
block. It must be
pointed out that the inverse transform must exist for unique
reconstruction. There are
a number of such transforms available in the field to choose from,
each having its own
merits and demerits. The most efficient transform is one that uses
the least number of
transform coefficients to reconstruct the image for a given amount
of distortion. Such
a linear transform is known as the optimal transform where
optimality is with respect
to the minimum mean square error between the original and
reconstructed images.
This optimal image transform is known by the names Karhunen–Lo`eve transform
(KLT) or Hotelling
transform. The disadvantage of the KLT is that the
transform
kernel depends on the actual image to be compressed, which
requires a lot more side
information for the receiver to reconstruct the original image
from the compressed
image than other fixed transforms. A highly popular fixed transform
is the familiar
discrete cosine transform (DCT). The DCT has very nearly the same compression
efficiencyas the KLT
with the advantage that its kernel is fixed and so no side information
is required by the receiver for the reconstruction. The DCT is
used in
the JPEG and MPEG video compression standards. The DCT is usually
applied on
nonoverlapping blocks of an image. Typical DCT blocks are of size
8 × 8 or 16 × 16.
One of the disadvantages of image compression using the DCT is the
blocking
artifact. Because the DCT blocks are small compared with the image
and because
the average values of the blocks may be different, blocking
artifacts appear when
the zero-frequency (dc) DCT coefficients are quantized rather
heavily. However, at
low compression, blocking artifacts are almost unnoticeable. An
example showing
blockingartifacts due to compression using 8 ×
8 DCT is shown in Figure 3 a.
Blockiness is clearly seen in flat areas—both low and high
intensities as well as undershoot
and overshoot along the sharp edges—see Figure 3 b. A listing of
M-file
for Figures
3 a,b is shown below.
Figure
3 (a) Cameraman image showing blocking artifacts due to quantization of the DCT
coefficients.
The DCT size is 8 × 8. (b) Intensity profile along row number 164 of the
image
in (a).
%
Figure3.m
%
Example to show blockiness in DCT compression
%
Quantizes and dequantizes an intensity image using
%
8x8 DCT and JPEG quantization matrix
close
all
clear
I
= imread(’cameraman.tif’);
figure,imshow(I),
title(’Original Image’)
%
fun
= @dct2; % 2D DCT function
N
= 8; % block size of 2D DCT
T
= blkproc(I,[N N],fun); % compute 2D DCT of image using NxN blocks
%
Scale
= 4.0; % increasing Scale quntizes DCT coefficients heavily
%
JPEG default quantization matrix
jpgQMat
= [16 11 10 16 24 40 51 61;
12
12 14 19 26 58 60 55;
14
13 16 24 40 57 69 56;
14
17 22 29 51 87 80 62;
18
22 37 56 68 109 103 77;
24
35 55 64 81 194 113 92;
49
64 78 87 103 121 120 101;
72
92 95 98 121 100 103 99];
Qstep
= jpgQMat * Scale; % quantization step size
%
Quantize and dequantize the coefficients
for
k = 1:N:size(I,1)
for
l = 1:N:size(I,2)
T1(k:k+N-1,l:l+N-1)
= round(T(k:k+N-1,l:l+N-1)./ Qstep).*Qstep;
end
end
%
do inverse 2D DCT
fun
= @idct2;
y
= blkproc(T1,[N N],fun);
y
= uint8(round(y));
figure,imshow(y),
title(’DCT compressed Image’)
%
Plot image profiles before and after compression
ProfRow
= 164;
figure,plot(1:size(I,2),I(ProfRow,:),’k’,’LineWidth’,2)
hold
on
plot(1:size(I,2),y(ProfRow,:),’-.k’,’LineWidth’,1)
title([’Intensity
profile of row ’ num2str(ProfRow)])
xlabel(’Pixel
number’), ylabel(’Amplitude’)
%legend([’Row’
’ ’ num2str(ProfRow)],0)
legend(’Original’,’Compressed’,0)
A third and relatively recent compression method is based on wavelet transform.
As we will see in a later chapter, wavelet transform captures both
long-term and
short-term changes in an image and offers a highly efficient
compression mechanism.
As a result, it is used in the latest versions of the JPEG
standards as a compression
tool. It is also adopted by the SMPTE (Society of Motion Pictures
and Television
Engineers). Even though the wavelet transform may be applied on
blocks of an image
like the DCT,
it is generally applied on the full image and the various wavelet
Figure
4.A two-level 2D DWT of cameraman image.
coefficients
are quantized according to their types. A two-level discrete wavelet transform
(DWT)
of the cameraman image is shown in Figure 1.6 to illustrate how the 2D
wavelet
transform coefficients look like. Details pertaining to the levels and subbands
of
the DWT will be given in a later chapter. The M-file to implement multilevel 2D
DWT
that generates Figure 5 is listed below. As we will see in a later chapter, the
2D
DWT decomposes an image into one approximation and many detail coefficients.
The
number of coefficient subimages corresponding to an L-level 2D DWT equals
3
× L + 1. Therefore, for a two-level 2D DWT, there are seven coefficient
subimages.
In
the first level, there are three detail coefficient subimages, each of size 14
the
original image. The second level consists of four sets of DWT coefficients—one
approximation
and three details, each 1
16
the original image. As the name implies the
approximation
coefficients are lower spatial resolution approximations to the original
image.
The detail coefficients capture the discontinuities or edges in the image with
orientations
in the horizontal, vertical, and diagonal directions. In order to compress,
an
image using 2D DWT we have to compute the 2D DWT of the image up to a given
level
and then quantize each coefficient subimage. The achievable quality and
compression
ratio
depend on the chosen wavelets and quantization method. The visual
effect
of quantization distortion in DWT compression scheme is different from that
in
DCT-based scheme. Figure 6 a is the cameraman image compressed using 2D
DWT.
The wavelet used is called Daubechies 2 (db2 in MATLAB) and the number
of
levels used is 1. We note that there are no blocking effects, but there are
patches
in
the flat areas. We also see that the edges are reproduced faithfully as
evidenced
in
the profile (Figure 6 b). It must be pointed out that the amount of quantization
applied
in Figure 6 a is not the same as that used for the DCT example and that the
two
examples are given only to show the differences in the artifacts introduced by
the
two schemes. An M-file listing to generate Figures 6 a,b is shown below
%
2D Discrete Wavelet Transform (DWT)
%
Computes multi-level 2D DWT of an intensity image
close
all
clear
I
= imread(’cameraman.tif’);
figure,imshow(I),
title(’Original Image’)
L
= 2; % number of levels in DWT
[W,B]
= wavedec2(I,L,’db2’); % do a 2-level DWT using db2 wavelet
%
declare level-1 subimages
w11
= zeros(B(3,1),B(3,1));
w12
= zeros(B(3,1),B(3,1));
w13
= zeros(B(3,1),B(3,1));
%
declare level-2 subimages
w21
= zeros(B(1,1),B(1,1));
w22
= zeros(B(1,1),B(1,1));
w23
= zeros(B(1,1),B(1,1));
w24
= zeros(B(1,1),B(1,1));
%
extract level-1 2D DWT coefficients
offSet11
= 4*B(1,1)*B(1,2);
offSet12
= 4*B(1,1)*B(1,2)+B(3,1)*B(3,2);
offSet13
= 4*B(1,1)*B(1,2)+2*B(3,1)*B(3,2);
for
c = 1:B(2,2)
for
r = 1:B(2,1)
w11(r,c)
= W(offSet11+(c-1)*B(3,1)+r);
w12(r,c)
= W(offSet12+(c-1)*B(3,1)+r);
w13(r,c)
= W(offSet13+(c-1)*B(3,1)+r);
end
end
%
extract level-2 2D DWT coefficients
offSet22
= B(1,1)*B(1,2);
offSet23
= 2*B(1,1)*B(1,2);
offSet24
= 3*B(1,1)*B(1,2);
for
c = 1:B(1,2)
for
r = 1:B(1,1)
w21(r,c)
= W((c-1)*B(1,1)+r);
w22(r,c)
= W(offSet22+(c-1)*B(1,1)+r);
w23(r,c)
= W(offSet23+(c-1)*B(1,1)+r);
w24(r,c)
= W(offSet24+(c-1)*B(1,1)+r);
end
end
%
declare output array y to store all the DWT coefficients
%y
= zeros(261,261);
y
= zeros(2*B(1,1)+B(3,1),2*B(1,2)+B(3,2));
y(1:B(1,1),1:B(1,1))=w21;
y(1:B(1,1),B(1,1)+1:2*B(1,1))=w22;
y(B(1,1)+1:2*B(1,1),1:B(1,1))=w23;
y(B(1,1)+1:2*B(1,1),B(1,1)+1:2*B(1,1))=w24;
%
y(1:B(3,1),2*B(1,1)+1:261)=w11;
y(2*B(1,1)+1:261,1:129)=w12;
y(2*B(1,1)+1:261,2*B(1,1)+1:261)=w13;
figure,imshow(y,[]),title([num2str(L)
’-level 2D DWT’])
%
Figure6.m
%
An example to show the effect of quantizing the 2D DWT
%
coefficients of an intensity image along with intensity
%
profile along a specified row
%
close
all
clear
I
= imread(’cameraman.tif’);
figure,imshow(I),
title(’Original Image’)
%
do a 1-level 2D DWT
[W,B]
= wavedec2(I,1,’db2’);
w11
= zeros(B(1,1),B(1,2));
w12
= zeros(B(1,1),B(1,2));
w13
= zeros(B(1,1),B(1,2));
w14
= zeros(B(1,1),B(1,2));
%
offSet12
= B(1,1)*B(1,2);
offSet13
= 2*B(1,1)*B(1,2);
offSet14
= 3*B(1,1)*B(1,2);
%
quantize only the approximation coefficients
Qstep
= 16;
for
c = 1:B(1,2)
for
r = 1:B(1,1)
W((c-1)*B(1,1)+r)
= floor(W((c-1)*B(1,1)+r)/Qstep)*Qstep;
%{
W(offSet12+(c-1)*B(1,1)+r)
= floor(W(offSet12+(c-1)*B(1,1)+r)/8)*8;
W(offSet13+(c-1)*B(1,1)+r)
= floor(W(offSet13+(c-1)*B(1,1)+r)/8)*8;
W(offSet14+(c-1)*B(1,1)+r)
= floor(W(offSet14+(c-1)*B(1,1)+r)/8)*8;
%}
end
end
%
do inverse 2D DWT
y
= waverec2(W,B,’db2’);
figure,imshow(y,[])
%
plot profile
ProfRow
= 164;
figure,plot(1:size(I,2),I(ProfRow,:),’k’,’LineWidth’,2)
hold
on
plot(1:size(I,2),y(ProfRow,:),’-.k’,’LineWidth’,1)
title([’Profile
of row ’ num2str(ProfRow)])
xlabel(’Pixel
number’), ylabel(’Amplitude’)
%legend([’Row’
’ ’ num2str(ProfRow)],0)
legend(’Original’,’Compressed’,0)
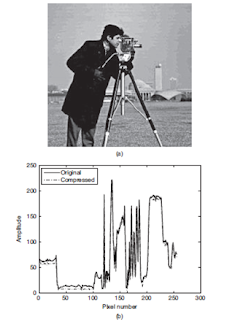
Figure 6(a)
Cameraman image compressed using one-level 2D DWT. (b) Intensity profile of
image .





No comments:
Post a Comment